| Enviar | Todos los envíos | Mejores soluciones | Atrás a la lista |
AI13_NEU - Neurografo |
Entre los jóvenes competidores del Abierto de Informática se encuentra un adolescente apasionado por la biología, Alex. Hace muy poco, mientras estudiaba el sistema nervioso, se encontró con que existían en él un tipo muy particular de células: las neuronas.
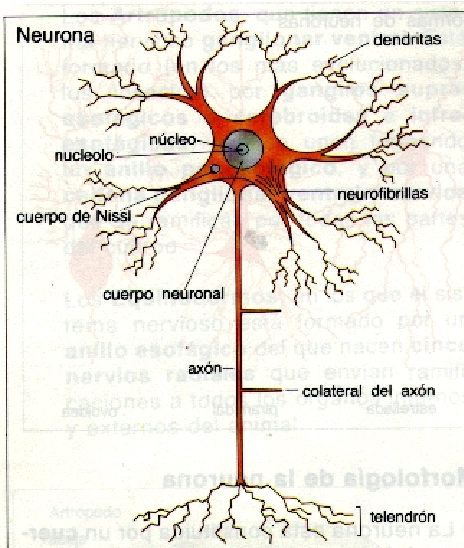
Una neurona tiene la capacidad de comunicarse con precisión, rapidez y a larga distancia con otras células, ya sean nerviosas, musculares o glandulares. Para que esto sea posible, consta de una zona de recepción y otra de emisión donde se encuentran las dendritas y el axón, sus elementos encargados de la recepción y el envío respectivamente.
Alex, curioso como es, descubrió que para facilitar el estudio de las inmensas redes neuronales que se pueden llegar formar, los bioinformáticos han creado un tipo de grafo especial para el caso, denominado neurografo. A diferencia de un grafo cualquiera, cumple con ciertas propiedades. De acuerdo a su definición:
- Tiene arcos bidireccionales no ponderados.
- Todos los nodos están conectados entre sí, ya sea directa o indirectamente. (Es decir, forman un componente conexo).
- Contiene exactamente un ciclo (ni cero, ni dos, ni tres, solamente uno).
Si bien esta simplificación ha permitido a los investigadores trabajar de una manera más cómoda, de vez en cuando surge entre ellos la necesidad de comprobar si un grafo no dirigido, obtenido por medio de otros estudios, contiene o no neurografos. Alex, ocioso como sólo él podría ser, pasó toda la tarde del día siguiente dibujando redes neuronales. Ahora se dispone a responder la misma pregunta que los investigadores:
Dado un grafo no dirigido no ponderado, conformado por uno o más componentes conexos, ¿cuántos de éstos componentes se pueden considerar neurografos?
Input
En la primera línea se encuentra un número NC, el número de casos de prueba. A continuación siguen NC casos de prueba.
Cada caso de prueba consiste de: Dos números en la primera línea N (1 ≤ N ≤ 10000) y M (1 ≤ M ≤ N * (N - 1) * 0.5), el número de nodos y el número de arcos respectivamente. A continuación se describen M arcos, representados por 2 números diferentes x,y (1 ≤ x, y ≤ N) que representan la conexión bidireccional entre los nodos x e y.
La entrada no contiene arcos repetidos.
Output
Por cada caso de prueba, imprimir el número de componentes conexos que son neurografos.
Sample test(s)
input5
3 3
1 2
2 3
3 1
4 4
1 2
2 3
3 4
4 1
3 2
1 2
2 3
6 6
1 2
2 3
2 5
3 4
3 5
5 6
6 6
1 2
2 3
3 1
4 5
5 6
6 4output1
1
0
1
2
Note
Un componente conexo es un (sub)grafo, en el cual, todos los nodos que lo componen están conectados entre si, ya sea a través de uno o más arcos.
| Adicionado por: | Gabriel Rea Velasco |
| Fecha: | 2013-10-12 |
| Tiempo límite: | 1s-6s |
| Límite del código fuente: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Lenguajes: | C CSHARP C++ 4.3.2 CPP CPP14 JAVA |
| Fuente: | Abierto de informática 2013 - Segunda fase |