La arqueóloga Benjamas está corriendo por su vida luego de haber estado investigando la misteriosa
ciudad subterránea de los cocodrilos. La ciudad tiene N cámaras. Existen M corredores que pueden ser
utilizados en ambos sentidos, cada uno conecta un par de cámaras diferentes. Huir a través de cada
corredor puede requerir diferentes cantidades de tiempo. Sólo K de las N cámaras contienen salidas,
por medio de las cuales se puede completar el escape. Benjamas comienza en la cámara 0. Ella desea
alcanzar una cámara de salida tan pronto como sea posible.
El cocodrilo guardia quiere evitar que Benjamas pueda escapar. Desde su guarida, el controla puertas
secretas que pueden bloquear cualquier corredor. Esto significa que, cuando el cocodrilo bloquea un
nuevo corredor, aquél que bloqueó anteriormente queda desbloqueado.
La situación de Benjamas puede ser descrita como sigue: Cada vez que ella trata de abandonar una cámara,
el cocodrilo guardia puede elegir bloquear alguno de los corredores adyacentes a éste. Benjamas entonces
elige alguno de los corredores que no estén bloqueados hacia la siguiente cámara. Una vez que Benjamas entra
en un corredor, el cocodrilo guardian no puede bloquearlo hasta que Benjamas entre en la siguiente cámara. Una
vez que llega a la siguiente cámara, el guardian puede elegir bloquear uno de los corredores adyacentes a la
cámara donde se encuentra Benjamas (incluso puede bloquear el corredor que acaba de utilizar Benjamas anteriormente),
y así sucesivamente.
A ella le gustaría tener un plan de escape sencillo por adelantado. Más aún, a ella le gustaría tener un plan
que le indique que hacer cuando llegue a una cámara. Sea A una de las cámaras. Si es una cámara de salida, no
se requieren instrucciones (obviamente), ella puede escapar de la ciudad. De cualquier otra forma, la instrucción
para la cámara A debe tener alguna de las formas siguientes:
* “Si llega a alcanzar una cámara A, tome el corridor que dirige hacia la cámara B. Sin embargo, si este corredor
está bloqueado, entonces tome el corredor hacia la cámara C.”
* “No se preocupe por la cámara A, de acuerdo al plan de escape usted no puede llegar ahí de ninguna forma.”
Note que en algunos casos (por ejemplo, si su plan lleva a Benjamas a un ciclo) el guardia puede prevenir que
Benjamas logre llegar a una salida. Un plan de escape es bueno si Benjamas tiene garantizado su escape luego
de una cantidad de tiempo finito, sin importar lo que haga el guardia. Para un plan de escape correcto, sea T
el menor tiempo tal que luego de ese tiempo T, Benjamas tiene garantizado su escape. En ese caso podemos decir
que, un buen plan de escape tiene tiempo T (the good escape plan takes time T).
Problema
Escribir un procedimiento travel_plan(N,M,R,L,K,P), con los siguientes parámetros:
* N: el número de cámaras. Las cámaras están numeradas desde 0 hasta N-1.
* M: el número de corredores. Los corredores están numerados desde 0 hasta M-1.
* R: un arreglo bidimensional de enteros representando los corredores. Para 0 ≤ i < M, el corridor i conecta dos
cámaras distintas R[i][0] y R[i][1]. No dos corredores se unen en el mismo par de cámaras.
L: es un arreglo unidimensional de enteros que contiene los tiempos requeridos para cruzar cada corredor.
Para 0 ≤ i < M, el valor 1 ≤ L[i] ≤ 1 000 000 000 es el tiempo requerido por Benjamas para cruzar el ith corredor.
* K: el número de cámaras de salida. Usted puede asumir 1 ≤ K < N.
* P: un arreglo unidimensional de enteros, con K enteros diferentes que indican las cámaras de salidas.
Para 0 ≤ i < K, el valor P[i] es el número de la ith cámara de salida. La cámara 0 nunca formará parte de las
cámaras de salida.
Su procedimiento debe retornar la minima cantidad de tiempo T para el cual exista un plan que pueda ser considerado
bueno y tome como tiempo T.
Usted puede asumir que cada cámara que no tiene salida tendrá al menos 2 corredores. Usted puede asumir también que
en cada caso de prueba existe un plan bueno con un T ≤ 1 000 000 000.
Ejemplos
Ejemplo 1
Considere el caso descrito en la Figura 1, donde N=5, M=4, K=3, y
0 1
0 2
R = 3 2
2 4
2
3
L = 1
4
1
P = 3
4
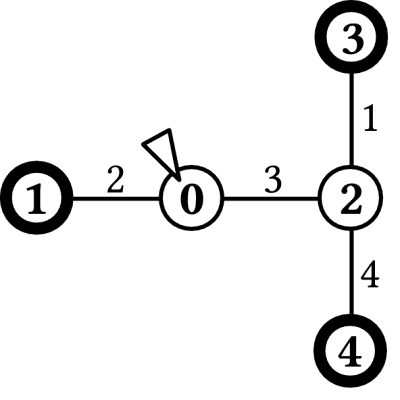Las cámaras son presentadas como círculos, y los corredores que las conectan son presentados como líneas. Las
cámaras de salida son resaltadas con los círculos gruesos. Benjamas comienza en la cámara 0 (marcada por un triángulo).
Un plan de escape optimal es el siguiente:
* Si usted llega a la cámara 0, toma el corredor hacia la cámara 1. Sin embargo, si ese corredor es bloqueado, entonces
debe tomar el corredor hacia la cámara 2.
* Si usted llega a la cámara 2, tome el corredor hacia la cámara 3. Sin embargo, si ese corredor está bloqueado, entonces
debe tomar el corredor hacia la cámara 4.
En el peor caso, Benjamas debe alcanzar su escape con un T=7, por ende, travel_plan debe retornar 7.
Ejemplo 2
Considere el caso descrito en la Figura 2, donde N=5, M=7, K=2, y
0 2
0 3
3 2
R= 2 1
0 1
0 4
3 4
4
3
2
L= 10
100
7
9
P= 1
3
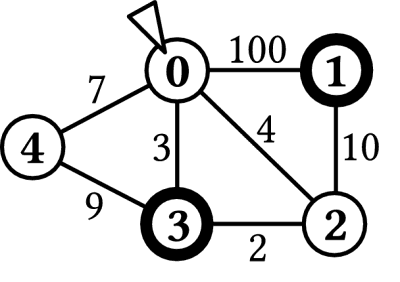Aquí se presenta el plan de escape optimal:
* Si usted alcanza la cámara 0, toma el corredor hacia la cámara 3. Sin embargo, si ese corredor está bloqueado,
entonces tome el corredor hacia la cámara 2.
* Si usted alcanza la cámara 2, tome el corredor hacia la cámara 3. Sin embargo, si ese corredor está bloqueado
tome el que lleva a la cámara 1.
* No se preocupe por la cámara 4, de acuerdo al plan usted no puede llegar ahí.
Benjamas alcanzará entonces una de las salidas antes de T=14. Entonces travel_plan debe retornar 14.
Las competencias en la IOI no requieren lectura/salida de datos estándar. Sin embargo,
el problema fue adaptado a la lectura de datos por entrada estándar.
El programa debe leer un único caso de prueba.
El pseudo-código para leer los datos de entrada es el siguiente:
leer(N,M,K)
for(i=0; i<M; i++){
leer(R[i][0],R[i][1],L[i])
}
for(i=0; i<K; i++){
leer(P[i])
}
La respuesta es impresa como siempre, por salida estándar.
Nota: A diferencia de otros problemas binarios de este juez, es decir, Aceptado/No Aceptado,
este problema tiene puntaje parcial sobre 100 puntos. Un algoritmo por fuerza bruta, obtendra unos
cuantos pero no muchos y un programa óptimo, recibirá la totalidad de los puntos.
A continuación se describe la distribución de los puntos para diferentes casos de prueba.
Subtarea 1
Subtarea 1 (46 puntos)
* 3 ≤ N ≤ 1 000.
* La ciudad subterranean es un árbol. Esto significa, M = N-1 y para cada par de cámaras i y j existe un camino simple entre i y j.
* Cada cámara de salida está conectada exactamente a otra cámara.
* Cualquiera de las otras cámaras está conectada directamente a 3 o más cámaras.
Subtarea 2 (43 puntos)
* 3 ≤ N ≤ 1 000.
* 2 ≤ M ≤ 100 000.
Subtarea 3 (11 puntos)
* 3 ≤ N ≤ 100 000.
* 2 ≤ M ≤ 1 000 000.
