Los elefantes danzantes es un espectacular show en Pattaya, donde N elefantes bailan
sobre una línea conocida como escenario.
Después de años de entrenamiento, los elefantes en este show son capaces de muchos bailes
increíbles. El espectáculo consta de una serie de actos. En cada acto, exactamente un (1) elefante
realiza un bello baile, mientras que, posiblemente puede moverse a una posición diferente.
Los productores del programa quieren elaborar un álbum de fotos que contiene imágenes de todo el
espectáculo. Después de cada acto, quieren tomar fotos de todos los elefantes tal y como son
vistos por los espectadores.
En cualquier momento durante el espectáculo, múltiples elefantes pueden compartir la misma posición.
En ese caso, simplemente se quedan detrás del otro en la misma posición.
Una sola cámara puede tomar una foto de un grupo de elefantes si y sólo si todas sus posiciones
se encuentran en un segmento de longitud L (incluyendo sus extremos). Como los elefantes pueden
extenderse por todo el escenario, varias cámaras podrían ser necesarias para tomar fotos simultáneas
de todos los elefantes.
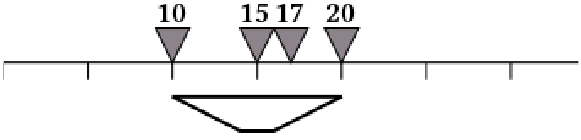
A modo de ejemplo, supongamos que L = 10 y que los elefantes se encuentran en las posiciones 10, 15, 17,
y 20 en el escenario. En este momento, una sola cámara puede tomar una foto, como se muestra a continuación.
(Los elefantes se muestran como triángulos, las cámaras se muestran como trapecios.)
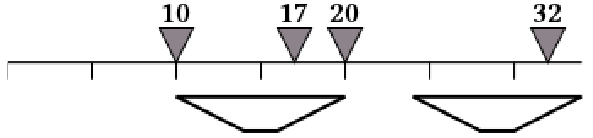
 En el siguiente acto, el elefante en la posición 15 baila hacia la posición 32. Después de este acto,
se necesitan al menos dos cámaras para tomar la foto.
En el siguiente acto, el elefante en la posición 15 baila hacia la posición 32. Después de este acto,
se necesitan al menos dos cámaras para tomar la foto.
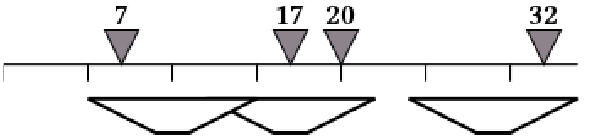
 En el siguiente acto, el elefante en la posición 10 se mueve hacia la posición 7. Para la nueva
disposición de los elefantes, se necesitan tres cámaras para fotografiar a todos ellos.
En el siguiente acto, el elefante en la posición 10 se mueve hacia la posición 7. Para la nueva
disposición de los elefantes, se necesitan tres cámaras para fotografiar a todos ellos.
 En esta tarea interactiva, tienes que determinar el número mínimo de cámaras necesarias para tomar
las fotos después de cada uno de los actos. Tenga en cuenta que el número de cámaras necesarias
puede aumentar, disminuir o permanecer igual entre los actos.
Problema
Escribe los siguientes procedimientos:
* Procedimiento init(N,L,X) que tenga los siguientes parámetros:
* N: el número de elefantes. Los elefantes son enumerados desde 0 hasta N-1.
* L: la longitud del segmento capturado por una sola cámara. Puedes asumir que 0 ≤ L ≤ 1.00.000.000
* X: un arreglo uni-dimensional representando las posiciones iniciales de los elefantes. Para 0 ≤ i < N, el elefante
i comienza en la posición X[i]. Las posiciones iniciales están ordenadas. Aun mas, Ud. puede asumir que
0 ≤ X[0] ≤ ... ≤ X[N-1] ≤ 1.000.000.000. Observa que durante el baile los elefantes pueden reordenarse ellos mismos.
Este procedimiento será ejecutado una sola vez antes de las llamadas a update. Este procedimiento no debe retornar nada.
* Procedimiento update(i,y) que tenga los siguientes parámetros:
* i: el número del elefante que se ha movido en el presente acto.
* y: la posición donde el elefante i deberá estar después del acto actual. Puedes asumir que 0 ≤ y ≤ 1.000.000.000
Este procedimiento será ejecutado múltiples veces. Cada llamada corresponde a un sólo acto (como el siguiente desde
todos los actos previos). Cada llamada debe retornar el mínimo número de cámaras necesarias para fotografiar a todos
los elefantes después del acto correspondiente.
Ejemplo:
Considera el caso donde N=4, L=10, y las posiciones iniciales de los elefantes son:
10
15
X= 17
20
Primero, tu procedimiento init(N,L,X) deberá ser llamado con estos parámetros. Luego tu procedimiento
update(i,y) será ejecutado una vez en cada acto. Aquí hay un ejemplo de la secuencia de llamadas y sus
correspondientes valores de retorno:
+-----+-----------------+--------------+
| act | call parameters | return value |
+-----+-----------------+--------------+
| 1 | update(2,16) | 1 |
| 2 | update(1,25) | 2 |
| 3 | update(3,35) | 2 |
| 4 | update(0,38) | 2 |
| 5 | update(2,0) | 3 |
+-----+-----------------+--------------+
Las competencias en la IOI no requieren lectura/salida de datos estándar. Sin embargo,
el problema fue adaptado a la lectura de datos por entrada estándar.
El programa debe leer un único caso de prueba.
El pseudo-código para leer los datos de entrada es el siguiente:
leer(N,L,M)
for(i=0; i<N; i++){
leer(X[i])
}
for(i=0; i<M; i++){
leer(ii[i],yy[i])
}
La respuesta es impresa como siempre, por salida estándar.
Nota: A diferencia de otros problemas binarios de este juez, es decir, Aceptado/No Aceptado,
este problema tiene puntaje parcial sobre 100 puntos. Un algoritmo por fuerza bruta, obtendra unos
cuantos pero no muchos y un programa óptimo, recibirá la totalidad de los puntos.
A continuación se describe la distribución de los puntos para diferentes casos de prueba.
Sub-tareas
Sub-tarea 1 (10 puntos)
* Aquí son exactamente N = 2 elefantes.
* Inicialmente y después de cada acto, las posiciones de todos los elefantes serán diferentes.
* Tu procedimiento update será llamado a los sumo unas 100 veces.
Sub-tarea 2 (16 puntos)
* 1 ≤ N ≤ 100
* Inicialmente y después de cada acto, las posiciones de todos los elefantes serán diferentes.
* Tu procedimiento update será ejecutado a los sumo 100 veces.
Sub-tarea 3 (24 puntos)
* 1 ≤ N ≤ 50.000
* Inicialmente y después de cada acto, las posiciones de todos los elefantes serán diferentes.
* Tu procedimiento update será llamado a los sumo unas 50.000 veces.
Sub-tarea 4 (47 puntos)
* 1 ≤ N ≤ 70.000
* Los elefantes pueden compartir la misma posición.
* Tu procedimiento update será llamado a lo sumo 70.000 veces.
Sub-tarea 5 (3 puntos)
* 1 ≤ N ≤ 150.000
* Los elefantes pueden compartir la misma posición.
* Tu procedimiento update será llamado a lo sumo 150.000 veces.
* Por favor, mira la nota sobre el ‘CPU time limit’ abajo en la sección siguiente.
En esta tarea interactiva, tienes que determinar el número mínimo de cámaras necesarias para tomar
las fotos después de cada uno de los actos. Tenga en cuenta que el número de cámaras necesarias
puede aumentar, disminuir o permanecer igual entre los actos.
Problema
Escribe los siguientes procedimientos:
* Procedimiento init(N,L,X) que tenga los siguientes parámetros:
* N: el número de elefantes. Los elefantes son enumerados desde 0 hasta N-1.
* L: la longitud del segmento capturado por una sola cámara. Puedes asumir que 0 ≤ L ≤ 1.00.000.000
* X: un arreglo uni-dimensional representando las posiciones iniciales de los elefantes. Para 0 ≤ i < N, el elefante
i comienza en la posición X[i]. Las posiciones iniciales están ordenadas. Aun mas, Ud. puede asumir que
0 ≤ X[0] ≤ ... ≤ X[N-1] ≤ 1.000.000.000. Observa que durante el baile los elefantes pueden reordenarse ellos mismos.
Este procedimiento será ejecutado una sola vez antes de las llamadas a update. Este procedimiento no debe retornar nada.
* Procedimiento update(i,y) que tenga los siguientes parámetros:
* i: el número del elefante que se ha movido en el presente acto.
* y: la posición donde el elefante i deberá estar después del acto actual. Puedes asumir que 0 ≤ y ≤ 1.000.000.000
Este procedimiento será ejecutado múltiples veces. Cada llamada corresponde a un sólo acto (como el siguiente desde
todos los actos previos). Cada llamada debe retornar el mínimo número de cámaras necesarias para fotografiar a todos
los elefantes después del acto correspondiente.
Ejemplo:
Considera el caso donde N=4, L=10, y las posiciones iniciales de los elefantes son:
10
15
X= 17
20
Primero, tu procedimiento init(N,L,X) deberá ser llamado con estos parámetros. Luego tu procedimiento
update(i,y) será ejecutado una vez en cada acto. Aquí hay un ejemplo de la secuencia de llamadas y sus
correspondientes valores de retorno:
+-----+-----------------+--------------+
| act | call parameters | return value |
+-----+-----------------+--------------+
| 1 | update(2,16) | 1 |
| 2 | update(1,25) | 2 |
| 3 | update(3,35) | 2 |
| 4 | update(0,38) | 2 |
| 5 | update(2,0) | 3 |
+-----+-----------------+--------------+
Las competencias en la IOI no requieren lectura/salida de datos estándar. Sin embargo,
el problema fue adaptado a la lectura de datos por entrada estándar.
El programa debe leer un único caso de prueba.
El pseudo-código para leer los datos de entrada es el siguiente:
leer(N,L,M)
for(i=0; i<N; i++){
leer(X[i])
}
for(i=0; i<M; i++){
leer(ii[i],yy[i])
}
La respuesta es impresa como siempre, por salida estándar.
Nota: A diferencia de otros problemas binarios de este juez, es decir, Aceptado/No Aceptado,
este problema tiene puntaje parcial sobre 100 puntos. Un algoritmo por fuerza bruta, obtendra unos
cuantos pero no muchos y un programa óptimo, recibirá la totalidad de los puntos.
A continuación se describe la distribución de los puntos para diferentes casos de prueba.
Sub-tareas
Sub-tarea 1 (10 puntos)
* Aquí son exactamente N = 2 elefantes.
* Inicialmente y después de cada acto, las posiciones de todos los elefantes serán diferentes.
* Tu procedimiento update será llamado a los sumo unas 100 veces.
Sub-tarea 2 (16 puntos)
* 1 ≤ N ≤ 100
* Inicialmente y después de cada acto, las posiciones de todos los elefantes serán diferentes.
* Tu procedimiento update será ejecutado a los sumo 100 veces.
Sub-tarea 3 (24 puntos)
* 1 ≤ N ≤ 50.000
* Inicialmente y después de cada acto, las posiciones de todos los elefantes serán diferentes.
* Tu procedimiento update será llamado a los sumo unas 50.000 veces.
Sub-tarea 4 (47 puntos)
* 1 ≤ N ≤ 70.000
* Los elefantes pueden compartir la misma posición.
* Tu procedimiento update será llamado a lo sumo 70.000 veces.
Sub-tarea 5 (3 puntos)
* 1 ≤ N ≤ 150.000
* Los elefantes pueden compartir la misma posición.
* Tu procedimiento update será llamado a lo sumo 150.000 veces.
* Por favor, mira la nota sobre el ‘CPU time limit’ abajo en la sección siguiente.
En el siguiente acto, el elefante en la posición 15 baila hacia la posición 32. Después de este acto, se necesitan al menos dos cámaras para tomar la foto.
En el siguiente acto, el elefante en la posición 10 se mueve hacia la posición 7. Para la nueva disposición de los elefantes, se necesitan tres cámaras para fotografiar a todos ellos.
En esta tarea interactiva, tienes que determinar el número mínimo de cámaras necesarias para tomar las fotos después de cada uno de los actos. Tenga en cuenta que el número de cámaras necesarias puede aumentar, disminuir o permanecer igual entre los actos. Problema Escribe los siguientes procedimientos: * Procedimiento init(N,L,X) que tenga los siguientes parámetros: * N: el número de elefantes. Los elefantes son enumerados desde 0 hasta N-1. * L: la longitud del segmento capturado por una sola cámara. Puedes asumir que 0 ≤ L ≤ 1.00.000.000 * X: un arreglo uni-dimensional representando las posiciones iniciales de los elefantes. Para 0 ≤ i < N, el elefante i comienza en la posición X[i]. Las posiciones iniciales están ordenadas. Aun mas, Ud. puede asumir que 0 ≤ X[0] ≤ ... ≤ X[N-1] ≤ 1.000.000.000. Observa que durante el baile los elefantes pueden reordenarse ellos mismos. Este procedimiento será ejecutado una sola vez antes de las llamadas a update. Este procedimiento no debe retornar nada. * Procedimiento update(i,y) que tenga los siguientes parámetros: * i: el número del elefante que se ha movido en el presente acto. * y: la posición donde el elefante i deberá estar después del acto actual. Puedes asumir que 0 ≤ y ≤ 1.000.000.000 Este procedimiento será ejecutado múltiples veces. Cada llamada corresponde a un sólo acto (como el siguiente desde todos los actos previos). Cada llamada debe retornar el mínimo número de cámaras necesarias para fotografiar a todos los elefantes después del acto correspondiente. Ejemplo: Considera el caso donde N=4, L=10, y las posiciones iniciales de los elefantes son: 10 15 X= 17 20 Primero, tu procedimiento init(N,L,X) deberá ser llamado con estos parámetros. Luego tu procedimiento update(i,y) será ejecutado una vez en cada acto. Aquí hay un ejemplo de la secuencia de llamadas y sus correspondientes valores de retorno: +-----+-----------------+--------------+ | act | call parameters | return value | +-----+-----------------+--------------+ | 1 | update(2,16) | 1 | | 2 | update(1,25) | 2 | | 3 | update(3,35) | 2 | | 4 | update(0,38) | 2 | | 5 | update(2,0) | 3 | +-----+-----------------+--------------+ Las competencias en la IOI no requieren lectura/salida de datos estándar. Sin embargo, el problema fue adaptado a la lectura de datos por entrada estándar. El programa debe leer un único caso de prueba. El pseudo-código para leer los datos de entrada es el siguiente: leer(N,L,M) for(i=0; i<N; i++){ leer(X[i]) } for(i=0; i<M; i++){ leer(ii[i],yy[i]) } La respuesta es impresa como siempre, por salida estándar. Nota: A diferencia de otros problemas binarios de este juez, es decir, Aceptado/No Aceptado, este problema tiene puntaje parcial sobre 100 puntos. Un algoritmo por fuerza bruta, obtendra unos cuantos pero no muchos y un programa óptimo, recibirá la totalidad de los puntos. A continuación se describe la distribución de los puntos para diferentes casos de prueba. Sub-tareas Sub-tarea 1 (10 puntos) * Aquí son exactamente N = 2 elefantes. * Inicialmente y después de cada acto, las posiciones de todos los elefantes serán diferentes. * Tu procedimiento update será llamado a los sumo unas 100 veces. Sub-tarea 2 (16 puntos) * 1 ≤ N ≤ 100 * Inicialmente y después de cada acto, las posiciones de todos los elefantes serán diferentes. * Tu procedimiento update será ejecutado a los sumo 100 veces. Sub-tarea 3 (24 puntos) * 1 ≤ N ≤ 50.000 * Inicialmente y después de cada acto, las posiciones de todos los elefantes serán diferentes. * Tu procedimiento update será llamado a los sumo unas 50.000 veces. Sub-tarea 4 (47 puntos) * 1 ≤ N ≤ 70.000 * Los elefantes pueden compartir la misma posición. * Tu procedimiento update será llamado a lo sumo 70.000 veces. Sub-tarea 5 (3 puntos) * 1 ≤ N ≤ 150.000 * Los elefantes pueden compartir la misma posición. * Tu procedimiento update será llamado a lo sumo 150.000 veces. * Por favor, mira la nota sobre el ‘CPU time limit’ abajo en la sección siguiente.
