El botánico Somhed regularmente lleva a sus estudiantes a uno de los jardines tropicales más
grandes de Thailandia. El jardín está compuesto por N fuentes (numeradas de 0 hasta N-1) y M
caminos. Cada camino conecta un par de fuentes distintas y pueden ser utilizados en ambas
direcciones. Además existe al menos un camino desde cada fuente. En cada camino hay hermosas
colecciones botánicas que Somhed le encantaría ver. Cada grupo puede comenzar su paseo desde
cualquiera de las fuentes.
Somhed adora las plantas tropicales. De acuerdo con ésto, desde cualquier fuente preferirá el
camino que posea las plantas más hermosas, a menos que ese sea el último camino utilizado y exista
un camino alternativo. De existir algún camino se tomará el segundo mejor camino. Por supuesto, si
no hay otra alternativa se devolverán utilizando el mismo camino que habían utilizado para llegar a
la intersección actual. Note que Somhed es un botánico profesional, y para él, no existen dos
caminos que tengan la misma belleza.
Sus estudiantes no están muy interesados en las plantas. Sin embargo, a ellos le encantaría tomar un
almuerzo en el restaurante Premium ubicado en la fuente P. Somhed sabe que sus estudiantes
tendrán hambre luego de tomar exactamente K caminos, donde K puede ser diferente para cada
grupo de estudiantes. Somhed se pregunta cuántas rutas diferentes puede recorrer con cada grupo de
estudiantes dadas las siguientes condiciones:
* Cada grupo puede comenzar desde cualquier fuente;
* Los caminos sucesivos deben ser elegidos de la forma descrita anteriormente; Y
* Cada grupo debe llegar a la fuente número P luego de utilizar exactamente K caminos.
Note que es válido pasar a través de la fuente P antes de finalizar la ruta, sin embargo, dicha ruta
debe terminar en la fuente P para ser considerada válida.
Problema
Dada la información de las fuentes y los caminos, usted debe encontrar las respuestas para Q grupos
diferentes de estudiantes, esto significa Q valores para K.
Escriba un procedimiento llamado count_routes(N,M,P,R,Q,G) que tenga los siguientes parámetros:
* N: número de fuentes. Las fuentes están numeradas de 0 hasta N-1.
* M : número de caminos. Los caminos están numerados desde 0 hasta M-1. Los caminos
serán indicados en orden decreciente de belleza: para todo 0 ≤ i < M-1, el camino i es más
hermoso que el camino i+1.
* P: la fuente donde está el restaurant Premium.
* R: una matriz representando los caminos. Para 0 ≤ i < M, el camino i conecta las fuentes
R[i][0] y R[i][1]. Recuerde que cada camino conecta dos fuentes distintas, y no existen 2
caminos que conecten el mismo par de fuentes.
* Q: número de grupos de estudiantes.
* G: es un arreglo unidimensional con los valores de K para cada grupo. Para 0 ≤ i < Q, G[i]
es el número de recorridos que el i-ésimo grupo debe tomar.
Para 0 ≤ i < Q, su procedimiento debe hallar el número posible de rutas con exactamente G[i]
caminos que el grupo i puede tomar para alcanzar la fuente P. Para cada grupo i, su procedimiento
debe llamar a answer(X) para indicar que el número de rutas es X. Las respuestas deben ser
entregadas en el mismo orden en que se encuentran los grupos. Si no existieran rutas válidas, su
procedimiento debe llamar a answer(0).
Ejemplos
Ejemplo 1
Considere el caso de la figura 1, donde N=6, M=6,
P=0, Q=1, G[0]=3, y
1 2
0 1
0 3
R= 3 4
4 5
1 5
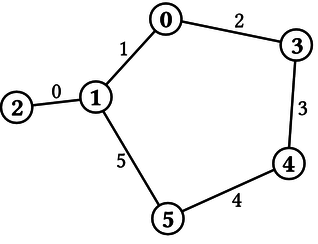Note que los caminos están listados en orden
decreciente de belleza. Esto significa que, el
camino 0 es el más hermoso, el camino 1 es el
segundo más hermoso y así sucesivamente.
Sólo existen dos rutas posibles de tamaño 3:
* 1 → 2 → 1 → 0, y
* 5 → 4 → 3 → 0.
La primera ruta comienza en la fuente 1. El camino más hermoso a partir de ahí los lleva a la fuente
2. En la fuente 2, el grupo no tiene mayor elección, deben retornar utilizando el mismo camino de
vuelta a la fuente 1. Luego desde esa fuente, el grupo no puede tomar el camino 0 dado que hay
alternativas y elige el camino 1 en su lugar. Este camino naturalmente los lleva a la fuente P=0.
Por tanto, el procedimiento debe hacer la llamada answer(2).
Ejemplo 2
Considere el caso de la figura 2, donde N=5, M=5, P=2, Q=2,
G[0]=3, G[1]=1, y
1 0
1 2
R= 3 2
1 3
4 2
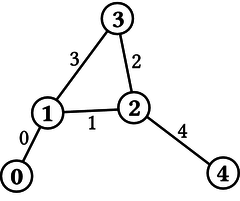Para el primer grupo, solo existe una ruta válida que alcanza
la fuente 2 luego de utilizar 3 caminos: 1 → 0 → 1 → 2.
Para el segundo grupo, existen 2 rutas válidas que alcanzan la fuente luego de utilizar 1 camino: 3 → 2, y 4 → 2.
Por tanto, la respuesta correcta de count_routes para este ejemplo debe llamar a answer(1) para
reportar el resultado del primer grupo y luego llamar a answer(2) para indicar la respuesta para el
segundo grupo.
Las competencias en la IOI no requieren lectura/salida de datos estándar. Sin embargo,
el problema fue adaptado a la lectura de datos por entrada estándar.
El programa debe leer un único caso de prueba.
El pseudo-código para leer los datos de entrada es el siguiente:
leer(N,M,P)
for(i=0; i<M; i++){
leer(R[i][0],R[i][1])
}
leer(Q)
for(i=0; i<Q; i++){
leer(G[i])
}
La respuesta es impresa como siempre, por salida estándar.
Nota: A diferencia de otros problemas binarios de este juez, es decir, Aceptado/No Aceptado,
este problema tiene puntaje parcial sobre 100 puntos. Un algoritmo por fuerza bruta, obtendra unos
cuantos pero no muchos y un programa óptimo, recibirá la totalidad de los puntos.
A continuación se describe la distribución de los puntos para diferentes casos de prueba.
Sub Tareas
Sub Tarea 1 (49 points)
* 2 ≤ N ≤ 1.000
* 1 ≤ M ≤ 10.000
* Q = 1
* cada elemento de G es un entero entre
1 y 100, inclusive.
Sub Tarea 3 (31 points)
* 2 ≤ N ≤ 150.000
* 1 ≤ M ≤ 150.000
* 1 ≤ Q ≤ 2.000
* cada elemento de G es un entero entre
1 y 1.000.000.000, inclusive.
Sub Tarea 2 (20 points)
* 2 ≤ N ≤ 150.000
* 1 ≤ M ≤ 150.000
* Q = 1
* cada elemento de G es un entero entre
1 y 1.000.000.000, inclusive.
