| Enviar | Todos los envíos | Mejores soluciones | Atrás a la lista |
TH_RACE - Race |
De manera simultánea con la IOI, la ciudad de Pattaya será anfitrión de la carrera:
International Olympiad in Racing (IOR) 2011. Como anfitriones debemos encontrar el
mejor recorrido para la carrera.
En el área metropolitana de Pattaya-Chonburi hay unas N ciudades conectadas por una red
de N-1 autopistas. Cada autopista es bidireccional, conecta a dos (2) ciudades diferentes y
se tiene su tamaño en kilómetros. Ademas, existe sólo un camino entre cualquier par de ciudades.
Esto es, existe exactamente una forma de viajar de una ciudad a otra utilizando una secuencia de
autopistas sin visitar la misma ciudad una o mas veces.
Por regulaciones específicas de la IOR requiere de un recorrido que mida exactamente K kilómetros,
iniciando y terminando en ciudades diferentes. Obviamente, ninguna autopista (y tampoco ninguna ciudad)
puede ser usada dos (2) veces por el recorrido para prevenir colisiones. Para minimizar las interrupciones
del tráfico en la ciudad el recorrido debe contener tan pocas autopistas como sea posible.
Problema
Escribe el procedimiento best_path(N,K,H,L) tal que tome los siguientes parámetros:
* N: el número de ciudades. Las ciudades son enumeradas desde 0 hasta N-1.
* K: la distancia requerida para el circuito de la carrera.
* H: un arreglo bidimensional representando las autopistas. Para 0 ≤ i < N-1, la autopista i conecta las
ciudades H[i][0] y H[i][1].
* L: un arreglo unidimensional que representa las longitudes de las autopistas. Para 0 ≤ i < N-1, la
longitud de la autopista i es L[i].
Debes asumir que todos los valores en el arreglo H están entre 0 y N-1, inclusive, y que las autopistas
descritas en dicho arreglo conectan todas las ciudades descritas anteriormente.
También debes asumir que todos los valores en el arreglo L son números enteros entre 0 y 1.000.000, inclusive.
Tu procedimiento debe retornar el mínimo número de autopistas dentro de un recorrido de exactamente longitud K.
Si resulta imposible construir dicho recorrido debes retornar -1.
Ejemplos
Ejemplo 1
Considere el caso mostrado en la Figura 1, donde N=4, K=3,
0 1
H= 1 2
1 3
1
L= 2
4
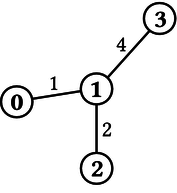 El circuito puede iniciarse en la ciudad 0, ir hacia la ciudad 1, y terminar
en la ciudad 2. La longitud será exactamente 1 km + 2 km = 3 km, y
esta ruta consiste de dos (2) autopistas. Esta es la mejor ruta posible; por
lo tanto best_path(N,K,H,L) debe retornar 2.
Ejemplo 2
Considera el caso mostrado en la Figura 2, donde N=3, K=3,
0 1
H= 1 2
L= 1
1
El circuito puede iniciarse en la ciudad 0, ir hacia la ciudad 1, y terminar
en la ciudad 2. La longitud será exactamente 1 km + 2 km = 3 km, y
esta ruta consiste de dos (2) autopistas. Esta es la mejor ruta posible; por
lo tanto best_path(N,K,H,L) debe retornar 2.
Ejemplo 2
Considera el caso mostrado en la Figura 2, donde N=3, K=3,
0 1
H= 1 2
L= 1
1
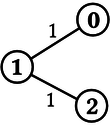 Este es un recorrido invalido. En este caso, best_path(N,K,H,L) debe retornar
-1.
Ejemplo 3
Considera el caso mostrado en la Figura 3, donde
N=11, K=12,
0 1
0 2
2 3
3 4
H= 4 5
0 6
6 7
6 8
8 9
8 10
3
4
5
4
L= 6
3
2
5
6
7
Este es un recorrido invalido. En este caso, best_path(N,K,H,L) debe retornar
-1.
Ejemplo 3
Considera el caso mostrado en la Figura 3, donde
N=11, K=12,
0 1
0 2
2 3
3 4
H= 4 5
0 6
6 7
6 8
8 9
8 10
3
4
5
4
L= 6
3
2
5
6
7
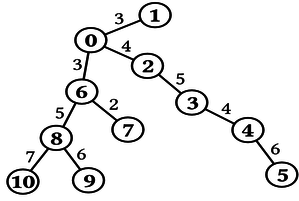 Un posible recorrido consiste de 3 autopistas: desde la ciudad 6 vía ciudad 0 y ciudad 2 hacia
ciudad 3. Otro posible recorrido se inicia en la ciudad 10 y pasa por la ciudad 8 hacia la cuidad 6.
Ambos recorridos tienen una longitud de 12 km como se requiere. El segundo recorrido es optimal,
por cuanto no hay un recorrido valido con una sola autopista. Finalmente best_path(N,K,H,L) debe
retornar 2.
Las competencias en la IOI no requieren lectura/salida de datos estándar. Sin embargo,
el problema fue adaptado a la lectura de datos por entrada estándar.
El programa debe leer un único caso de prueba.
El pseudo-código para leer los datos de entrada es el siguiente:
leer(N,K)
for(i=0; i<N-1; i++){
leer(H[i][0],H[i][1],L[i])
}
La respuesta es impresa como siempre, por salida estándar.
Nota: A diferencia de otros problemas binarios de este juez, es decir, Aceptado/No Aceptado,
este problema tiene puntaje parcial sobre 100 puntos. Un algoritmo por fuerza bruta, obtendra unos
cuantos pero no muchos y un programa óptimo, recibirá la totalidad de los puntos.
A continuación se describe la distribución de los puntos para diferentes casos de prueba.
Subtreas
Subtarea 1 (9 puntos)
* 1 ≤ N ≤ 100
* 1 ≤ K ≤ 100
* La red de autopistas forman una simple linea: para , 0 ≤ i < N-1, la autopista i conecta las ciudades i y i+1.
Subtarea 2 (12 puntos)
* 1 ≤ N ≤ 1.000
* 1 ≤ K ≤ 1.000.000
Subtarea 3 (22 puntos)
* 1 ≤ N ≤ 200.000
* 1 ≤ K ≤ 100
Subtarea 4 (57 puntos)
* 1 ≤ N ≤ 200.000
* 1 ≤ K ≤ 1.000.000
Un posible recorrido consiste de 3 autopistas: desde la ciudad 6 vía ciudad 0 y ciudad 2 hacia
ciudad 3. Otro posible recorrido se inicia en la ciudad 10 y pasa por la ciudad 8 hacia la cuidad 6.
Ambos recorridos tienen una longitud de 12 km como se requiere. El segundo recorrido es optimal,
por cuanto no hay un recorrido valido con una sola autopista. Finalmente best_path(N,K,H,L) debe
retornar 2.
Las competencias en la IOI no requieren lectura/salida de datos estándar. Sin embargo,
el problema fue adaptado a la lectura de datos por entrada estándar.
El programa debe leer un único caso de prueba.
El pseudo-código para leer los datos de entrada es el siguiente:
leer(N,K)
for(i=0; i<N-1; i++){
leer(H[i][0],H[i][1],L[i])
}
La respuesta es impresa como siempre, por salida estándar.
Nota: A diferencia de otros problemas binarios de este juez, es decir, Aceptado/No Aceptado,
este problema tiene puntaje parcial sobre 100 puntos. Un algoritmo por fuerza bruta, obtendra unos
cuantos pero no muchos y un programa óptimo, recibirá la totalidad de los puntos.
A continuación se describe la distribución de los puntos para diferentes casos de prueba.
Subtreas
Subtarea 1 (9 puntos)
* 1 ≤ N ≤ 100
* 1 ≤ K ≤ 100
* La red de autopistas forman una simple linea: para , 0 ≤ i < N-1, la autopista i conecta las ciudades i y i+1.
Subtarea 2 (12 puntos)
* 1 ≤ N ≤ 1.000
* 1 ≤ K ≤ 1.000.000
Subtarea 3 (22 puntos)
* 1 ≤ N ≤ 200.000
* 1 ≤ K ≤ 100
Subtarea 4 (57 puntos)
* 1 ≤ N ≤ 200.000
* 1 ≤ K ≤ 1.000.000
| Adicionado por: | Gabriel Rea Velasco |
| Fecha: | 2013-08-30 |
| Tiempo límite: | 1s |
| Límite del código fuente: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Lenguajes: | C CSHARP C++ 4.3.2 CPP CPP14 JAVA |
| Fuente: | IOI 2011 - Thailand - Day 1 |
ocultar comentarios
|
2014-02-26 04:22:10 Daydreamer
Estimado Rolando, preocupase primero por dejar de hacer trampa en todo y completar lo que le falta a usted. No se preocupe por mi, no me rendiré. |
|
|
2014-02-25 12:07:04 Unsigned Team (Ronaldo)
Vamos Mauri nose rinda xD Última edición: 2014-02-25 12:07:23 |
|
|
2013-09-12 04:28:31 Daydreamer
Hay que añadir el pseudocodigo de lectura de datos a la respuesta?? |
|
|
2013-09-06 16:03:52 Daydreamer
Los gráficos de los ejemplos 2 y 3 están al revez cierto?? ^-^ |
